從一道數學題目看“轉化思想”

從一道數學題目看“轉化思想”

　　從一道數學題目看“轉化思想”

　　劉 偉

　　（浙江省杭州外國語學校）

　　我們在解決數學問題時，常常把有待解決或難以解決的問題，通過某種轉化手段，使它轉化成已經解決或比較容易解決的問題，從而求得原問題的解答，這里運用的就是轉化思想。教育家維果茨基認為，學生發展具有兩種水平：一是已經達到的發展水平，二是可能達到的發展水平。從某種程度上來說，轉化思想就是從“已達到的發展水平”，上升到“可達到的發展水平”，使學生在原有的基礎上，提高分析和解決問題的能力。

　　題目：設x，y是正實數，求代數式的

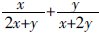
最大值。

　　此題屬于基本不等式范疇，但形式上看又有差距，需要進行一定的轉化變形，將未知轉化為已知是解決此題的關鍵。

　　一、利用整體思想轉化為基本不等式

　　二、通過分離常數轉化為基本不等式

　　三、通過換元轉化為函數的最值

　　此問題中有兩個未知數，而且兩未知數不存在等量關系，不能通過常規的“代入法”達到消元的目的。仔細觀察代數式，我們注意到兩個分式的分子、分母都是x，y一次關系式，利用分式的基本性質，將分子、分母同時除以x（或y），則可化為關于x/y的函數。

　　由已知條件x，y是正實數，分子、分母同除以x得：

　　四、回顧反思

　　布盧姆在《教育目標分類學》明確指出：數學轉化思想是“把問題元素從一種形式向另一種形式轉化的能力”。如果學生在掌握雙基的同時，接受了數學思想，學會了數學方法，就能激發學習數學興趣，提高分析問題和解決問題的能力，并為以后的數學學習打下堅實的基礎。本例是從聯想的角度，借助整體思想、換元等技巧實現轉化。在面對一個陌生的問題時，學生往往不能馬上找到解決之法，而是在直覺選擇的基礎上，通過聯想、化歸與構建的過程來確定解題的識別點。“遇新思陳、推陳出新、舉一反三”就是要在當前問題與頭腦中已有經驗之間建立聯系。無論在什么情況下都應該清醒地看到，所積累的知識和經驗都是解決問題的根本，善于轉化，很多問題都是可以迎刃而解的。

【從一道數學題目看“轉化思想”】相關文章：

淺談初中數學中數形思想轉化08-09

數學教案－因式分解中轉化思想的應用08-16

微軟公司的一道經典招聘題目08-17

作文構思訓練要培養轉化思想08-17

如何轉化數學差生08-08

淺談數學學困生的轉化08-17

如何轉化數學學困生08-18

一道有趣的數學作文02-02

因式分解中轉化思想的應用 —— 初中數學第一冊教案08-16

對一道數學題的思考08-08